Week 2: Exploring Methods
Our Goal (to reiterate)
We have the raw news data time series: \(\{\textbf{r}_n\}_{n=0}^{M}, \textbf{r}_t\in R\), where \(R\) is a 54-tuple over mostly categorical variables and we have \(M\) news history.
We also have \(\{x_t^{(i)}\}_{t=t_0-N}^{t_0}\), the time series data for EOD commodity price of the \((i)\)-th commodity on the \(t\)-th day, in \(\mathbb{R}_+\).
Initially, we’ll be trying just to find, for a given \(i\), \(f(\{\textbf{r}_n\}_{n\,=\,0}^{M},\{\textbf{x}_t\}_{t\,=\,t_0-N}^{t_0})\approx \mathbb{P}\left(x_{t+1}^{(i)}>x_{t}^{(i)}\right)\).
Approach
- Previous exploration has indicated there is some aspect of lower dimenality in \(R\) - agents would only interact with a small subset of other agents, each agent would only be affected by small subsets of types of events. Thus we’d like to reduce from \(R\) to \(\mathbb{R}^d\) for \(d < \dim R\).
- Evaluate what features we can extract from \(\{\textbf{x}_t\}_{t\,=\,t_0-N}^{t_0}\) alone - according to previous readings, summary statistics, such as moving averages, have some predictive power.
- Develop our forecasting model - consider the various regression methods for finding \(f\).
Part 1: Dimensionality Reduction
Reducing Categorical Data
Easy Removals
Some columns are redundant or don’t provide info:
GLOBALEVENTID– removedSQLDATEMonthYear– removedYear– removedFractionDate– removedDATEADDED– removedEventCode–EventRootCodeandEventBaseCodeare derived from it. CAMEO codes have three levels, and we want to be able to capture that lexicographic structure (decompose into 3-tier levels).URL– contains lots of trash; only use domain name for credibility detection.
Categorical Data Dimensionality Reduction
We will find it useful to define two functions, not necessarily related to each other:
- Define a metric \(\rho:R\times R\rightarrow \mathbb{R}_+\)
- Define an inner product \(\langle\cdot,\cdot\rangle:R\times R\rightarrow\mathbb{R}\)
The inner product induces the similary matrix \(G\in\mathbb{R}^{M\times M}\).
The assumption after the “easy removals” section above is that each of the columns contribute to the similarity and distance independently - so we only need to find per-column distances and similarities. It’s unlikely that we can find the ideal distance function manually, so it’s a good idea to parameterize it. These are going to end up being hyperparameters in the global regression problem, so we should be thrifty with them. One essential set of hyperparameters is the weights of each column. Other than that all the below functions can be extended to rely on additional hyperparameters if necessary.
We go through every column and define each columns own distance or similarity, each with its own parameters. For columns that are already numeric (e.g., NumArticles), that column’s contribution is just the \(L_1\) norm.
Categorical distances. We can probably come up with fancy distance metrics - QuadClass is one of {Verbal Cooperation, Material Cooperation, Verbal Conflict, Material Conflict}. One can make the argument that distance between “cooperation” is smaller than that between “verbal” and “material”, but we must be careful not to inject unvalidated parameters into the function - e.g., distance between conflict/cooperation is 2 but between verbal/material is 1.
Thus, for now, categorical variables will just operate on the discrete metric (with similarity being equal to distance).
Example of future potential improvement: look up location data - in addition to a discrete metric, “New York” and “Connecticut” string locations would have additional columns for their lattitude and longitude (which would have to be looked up).
Data Size
It is important to consider data size for feasibility of methods. For initial approaches, we’re going to use whole matrix representations, so we need to hold all \(N^2/2\) doubles in memory. At 8B for a packed double, when we’re testing on our machines, we’re already limited to 2*sqrt(8GB/8B), or only about ~60K rows!
Remember every recent day is about 200K rows.
Solutions:
- Most recent
~100rows, then randomly sample (we can weigh sampling by a function of the columns, since this is a linear-in-size operation) from previous days’ rows. Then we would sample about60Krows - Use
cycles.cs.princeton.edu, with256GBram, boosting us to~200Krows, but this is still barely a day’s worth. Would need to use sampling again. - Read data into a
LevelDBinstance, then reply to distance/dissimilarity queries on demand.
Last one is a lot of work, but probably the most enabling. Note it does us pretty much no good if the algorithm needs to use \(O(M^2)\) space.
Linear or Locally Linear Approaches
Linear dimensionality reduction approaches all rely on finding a projection matrix \(P\) and then offering \(PX\) as the reduced data. LLE is somewhat similar (see below).
-
Principal Components Analysis
Cunningham and Ghahramani 2015, Section 3.1.1. Classical PCA minimizes the sum of the squares of the residuals over all projections of the data into a low dimensional space. Usual matrix solution is to take SVD of \(G=Q\Lambda Q^\top\), then the first \(r\) columns.
Works well when data lie near (in terms of square distance) a low-dimensional hyperplane.
If PCA works the best out of all of these, we can extend to Probabilistic or Bayesian PCA.
-
Multidimensional Scaling
Cunningham and Ghahramani 2015, Section 3.1.2. MDS maximizes scatter (sum of pairwise distances). Optimizes
\[\min_{\textbf{s}_i}\sum_{i,j}\left(\|\textbf{s}_i-\textbf{s}_j\|_2-\rho(\textbf{r}_i,\textbf{r}_j)\right)^2\]Works well when that the most of the magnitude of the difference vectors between points lies in the vector spaced produced by the solution hyperplane.
Incremental MDS algorithms exist - this helps avoid quadratic space cost (on-demand \(\rho\)) but the runtime is still superquadratic.
-
Locally Linear Embedding
Roweis and Saul 2000. LLE is a nonlinear method which maintains the following invariant: for each data point’s closest \(K\) neighbors, the local linear approximation of the original point is maintained after the mapping.
Assumes that the points lie near some differentiable manifold in the the high-dimensional space, and performs well for manifolds isomorphic to a hyperplane.
Uh-oh! Note we only have \(G=XX^\top\), not \(X\), to work with! So even if we find \(P\), what would we apply it to? We need some initial mapping \(k:R\rightarrow\mathbb{R}^D\) which respects \(G\). At that point the reduction is just \(PK\), where \(\boldsymbol{\delta}_n^\top K=k(\textbf{r}_n)^\top\). \(D\) should be approximately equal to the number of columns (our original dimension), but it’s a pretty hard problem to reconstruct \(X\) for small \(D\) from \(G\).
If \(D=M\), it’s easy - that’s just the Cholesky Decomposition. However, then our data matrix is just as large as our Gram matrix, and this isn’t very scalable.
This leaves us with the following options:
- For small \(M\), during our exploratory stage, just use the entire \(M\times M\) data matrix, since we’re holding \(G\) in memory already anyway.
- Bite the bullet, and use a one-hot encoding for our categories. We have a lot of categories. The URL column and actor names, even if we clean the URL, will contribute to having on the order of 20K columns - an all-double encoding means
160KBper row - a smarter 1-bit encoding is about12KB. Overall for 200 days we’d need0.5TB! - Use Rectangular Cholesky Decomposition for an approximate reconstruction in \(\mathbb{R}^D\) for \(D\) approximately equal to number of columns. This algorithm has a runtime of \(O(dM^2)\), with operations being array accesses and math (and this means DB/disk accesses). Even an optimized solution in
C++would take on the order of \((200\, \text{days} \times 200\, \text{Krows/day})^2 \times 10\, \text{us} = 1000\, \text{days}\) (LevelDB random access time).
Basically, we’re going to have to subsample no matter what. It’s probably possible to massively parallelize these computation, but that would be a tremendous engineering effort.
Neighborhood Embedding
-
t-Distributed Stochastic Neighbor Embedding
L.J.P. van der Maaten 2014. Probably, coupled with
LevelDBdatabase layer and a query-on-demand distance function \(\rho\), this is our best bet. t-SNE finds an embedding in \(O(M \log M)\) time in \(O(M)\) memory.t-SNE works by minimizing the KL-divergence between two distributions: \(P\), which represents pairwise similarity between data points of the high dimensional data, and \(Q\), for the low dimensional data. Minimizing \(KL(P\|Q)\) then gives us the distribution that requires the least amount of additional bits of information to infer pairwise similarity to \(P\) - like an informational analogue to MDS.
\(P\) and \(Q\) are defined in the paper - they are distributions over the point similarities themselves - in other words, \(p_{ij}\) is the probability that points \(i,j\) are similar, defined with ratios of Gaussian kernels of \(i,j\) to the kernels with everything else (see paper for exact definition). \(q_{ij}\) uses a heavier-tailed Student-t kernel to allow for far points in the high dimensions to be further appart in the lower dimension without as much KL penality. This helps address the curse of high dimensionality and focus on local structure.
Looks like our best bet, and enables us to use the full data set without subsampling.
Isomap
General approach, really it just transforms \(\rho\) into \(\rho'\), and can be used in addition to t-SNE or MDS.
Tenenbaum, Silva, and Langford 2000. Isomap works by taking a neighborhood graph, then recomputing distances based on the shortest path through the neighborhood graph, and then applying classical reduction techniques. Thus we can only traverse to nodes through neighbors. This enlarges distances to be more “intrinsic” to our manifold:
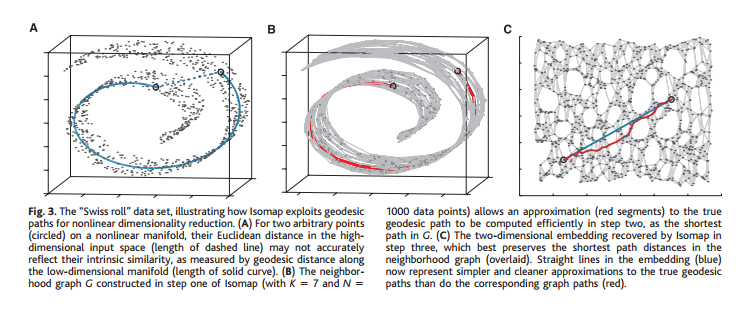
Isomap doesn’t have the same requirement of hyperplane isomorphism that LLE does, but needs a shortest path computation over all nodes for the new metric it uses. This is done by the Floyd–Warshall algorithm, but in \(O(M^3)\).
Implementation
Python’s sklearn has all of the above methods (except t-SNE, which has optimized CUDA implementations). Given that we have to deal with quadratic runtime in most of the preprocessing methods, the runtime of (1) and (2) is not a big deal. If we go with the column-based approach, then data-construction is linear, in which case maybe only LLE is tractable.
Evaluation Algorithm
Let us presume a probabilistic forcast \(f\) from above.
Matrix-based evaluation.
Outer loop: Take \(N'\) most recent rows and sample \(N\) more from \(M\) months ago. Run dimensionality reduction algorithm \(i\) from above.
Inner loop: Binary search on sub-dimension \(d\) (just a bias-variance tradeoff as we go low-to-high dimension, perhaps use F-score here in the binary search). Use the output of \(i\) on a given \(d\) to train and validate \(f\), obtaining some loss value.
Optimize the inner loop (logarithmic search over values \(1,...50\)) over hyperparameters \(N,N',M,i\). \(i\in\{1,...,4\}\) is small enough, but \(N,N',M\) need to be segmented (since they need to sweep a large range).
Distanced-based evaluation.
The only difference here is we’re looking up the rows and recomputing distance each time it is queried, not explicitly representing it. The outer loop’s parameters can be simplified to us the last \(N\) rows, where \(N\) may now be much larger.
Parts 2 and 3: Forecasting
Singapore Paper Recap
Forecasting Foreign Exchange Rates with Neural Networks
Models
Four input models
- time-delayed daily averages
- time-delayed weekly averages
- progressive averages (6 months back): day before, two days, week, 2 weeks, month, 3 months, 6 months
- long progressive averages (2 years back)
Cannot just rely on NMSE, need to evaluate models using profit
Profit = (money obtained / seed money)^{52/w} - 1
Two strategies: buying and selling whole amount when increase/decrease predicted, and buying/selling only 10% at a time
Results
- Predictions often much lower than real value or lagged behind forex rates
- Predicting longer than 6 months is hard (NMSE and profit diverge wildly)
- Profit decreases when training model further
- Experimenting with large number of currencies without inputting linkage is not good
- Best profits achieved with time-delayed 14 daily averages (which was also worst in terms of NMSE)
- Long progressive averages model is best for NMSE
- Boolean indicators help with NMSE but have no effect on profit
Feature selection
- The moving average of 1 week, 1 month, 3 months to smooth the price time series, for different commodities
- The (real valued) output from the dimensionality reduction of the GDELT.
Loss function
- \(L_2\) error between the real price movements and the prediction of the estimator
- Logarithmic Loss
Algorithms
We want to forecast the probability of direction changes using logit rather than linear functions, mainly because linear functions might result in degenerate solutions. Logit functions will map to [0,1], whereas a linear function might return something outside this range, unless we provide constraints. A linear function might still be useful for predicting probabilities within a general range of [0.2, 0.8], but will deviate greatly at extreme ranges, which we expect to encounter in our data. Whether or not the actual returns are linear or nonlinear is somewhat of an open question, with many types of models having been attempted with varying success.
Linear models
\(O^j_{t+1} := (x_{t+1}^{(i)} > x_t^{(i)}) = f(A_t \text{Data}_t)\)
Optimize the likelihood of what we see
- LDA, Maximum Likelihood … \(\text{max} \mathbb{P} (\text{Data}_t | O_t)\)
Optimize the prediction power over the training set
- Linear regression
- SVM: can also be non linear using a kernel
###Other Techniques
#####Hidden Markov Models
- A stochastic HMM-based forecasting model for fuzzy time series
- Need to define our hidden states, output states, transition probabilities between states
- Hidden states will correspond to market regimes (bullish, bearish)
- Can experiment with subsets of output states: large change up, slight change up, large change down, slight change down, no change
- Given past time series data we want to input a new data point (some news event) which might change our regime/hidden state
- Use generalized expectation-maximization to compute maximum likelihood estimates and posterior estimates for transitions and outputs
Fuzzification
- We want to predict financial time series movement
- Is it enough to stop at predicting price up vs price down?
- Fuzzification of Discrete Attributes From Financial Data in Fuzzy Classification Trees
- Piramuthu 1999, Kodogiannis and Lolis 2002, Lai et al 2009, Chen 2011
- After fuzzification and prediction, defuzzify to retrieve nonfuzzy prediction
- Allows for human domain knowledge to influence system
#####Nearest Neighbor
- Fuzzy Nearest-Neighbor Method for Time Series Forecasting
- Encode time series as vector of change in direction
- If \(x_{t} < x_{t-1} \implies -1\), if \(x_{t} > x_{t-1} \implies 1\), if \(x_{t} = x_{t-1} \implies 0\)
- Fuzzify and normalize data
- \[\mu(x_{i}) = [1 + \{d(x_{i}, x_{n}) / F(d)\}^{F_{e}}]^{-1.0}\]
- Select nearest neighbors that have a fuzzy proximity within a certain \(\epsilon\)
- Can also modify algorithm to have constraints where local movement around nearest neighbors must match prediction point
- Singh achieved directional success of 85% with \(\epsilon = 0.1, 0.2\) for product prices
#####Neural networks
- A new hybrid artificial neural networks and fuzzy regression model for time series forecasting
- The application of neural networks to forecast fuzzy time series
- Like the Fuzzy Nearest Neighbor, NNs have been adapted to use fuzzy logic
- Select some membership function \(\mu(x)\)
- Create rules based on membership values of time series points
- If \(x = A_{1}\) and \(y = B_{1} \implies f_{1} = p_{1}x + q_{1}y + r_{1}\)
- If \(x = A_{2}\) and \(y = B_{2} \implies f_{2} = p_{2}x + q_{2}y + r_{2}\)
- \(A_{i}\) and \(B_{i}\) are fuzzy sets
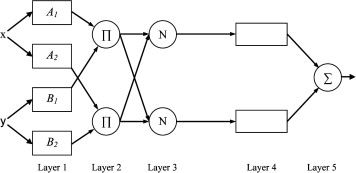
#####Genetic Algorithms
- Used to optimize parameters of neural nets, decision trees, etc
Result validation
- Divide the set in two: training and testing
- Cross validation doesn’t always make sense (look ahead bias)
- Develop a trading strategy and use on the market
We care about profit rather than model error. We can define a profit function as follows:
\(\begin{equation}
\text{Profit} = \Big(\dfrac{\text{money obtained}}{\text{seed money}}\Big)^{\dfrac{52}{w}} - 1
\end{equation}\)
where we use our model to invest a fixed variable percentage of our money on a weekly basis.
Most related work uses model error, which we can compare with, but few researchers have put forth actual profit numbers (most likely the problem is fairly hard).