Non-convex First Order Methods

This is a high-level overview of the methods for first order local improvement optimization methods for non-convex, Lipschitz, (sub)differentiable, and regularized functions with efficient derivatives, with a particular focus on neural networks (NNs).

\[ \argmin_\vx f(\vx) = \argmin_\vx \frac{1}{n}\sum_{i=1}^nf_i(\vx)+\Omega(\vx) \]

Make sure to read the general overview post first. I’d also reiterate as Moritz Hardt has that one should be wary of only looking at convergence rates willy-nilly.

Notation and Definitions.

• The \(t\)-th step stochastic gradient of \(f:\R^d\rightarrow\R\), computed in \(O(d)\) time at the location \(\vx_{t}\), by selecting either a single \(f_i\) or a mini-batch, is denoted \(\tilde{\nabla}_t\), with \(\E\tilde{\nabla}_t=\nabla_t=\nabla f(\vx_t)\).
• Arithmetic operations may be applied elementwise to vectors.
• If smooth and efficiently differentiable, e.g., \(\Omega(\vx)=\frac{1}{2}\norm{\vx}_2^2\), regularization can be folded into each \(f_i\) to make new \(f_i’=f_i+\frac{1}{n}\Omega\), as if it was never there in the first place. However, we may wish to apply \(L^1\) regularization or other non-smooth, non-differntiable but still convex functions–these are the problems I’ll label composite.
• I’ll use \(x\simeq y\) to claim that equality holds up to some fixed multiplicative constants.
• I will presume an initialization \(\vx_0\) (see discussion here).

• Finally, recall the two stationary point conditions:

  • \(\epsilon\)-approximate critical point: \(\norm{\nabla f(\vx_*)}\le \epsilon\)
  • \(\epsilon\)-approximate local minimum: there exists a neighborhood \(N\) of \(\vx_*\) such that for any \(\vx\) in \(N\), \(f(\vx)-f(\vx_*)\le \epsilon\). For \(f\) twice-differentiable at \(\vx_*\), it suffices to be an \(\epsilon\)-approximate critical point and have \(\nabla^2 f(\vx_*)\succeq \sqrt{\epsilon}I\).
• In this post, many algorithms will depend on a fixed learning rate, even if it’s just an initial scale for the learning rate. Convergence is sensitive to this setting; a fixed recommendation will surely be a poor choice for some problem. For a first choice, setting \(\eta\) to one of \( \{0.001,0.01,0.1\}\) based on a guess about the magnitude of the smoothness of the problem at hand is a good bet.

Stochastic Gradient Descent (SGD)

\[ \vx_{t+1}=\vx_t-\eta_t\tilde{\nabla}_t \]

Description. See Ghadimi and Lan 2013a for analysis and TensorFlow’s non-composite/composite implementation. The intuition behind SGD is to travel in a direction we expect is downhill, at least from where we are now. Put another way, the gradient defines a local linear approximation to our function, and we head in the direction that most directly lowers the cost for that approximation. The learning rate \(\eta_t\) controls how far against the gradient we’d like to go (before we judge the linear approximation to be inaccurate).

Assumptions. SGD makes the gradient estimation assumption, that \(\tilde{\nabla}_t\) is an unbiased estimator of \(\nabla_t\) with variance globally bounded, and the assumes that \(f\) is \(L\)-gradient-Lipschitz. Ghadimi et al 2013 extend to composite costs.

Guarantees. For a fixed-rate, \(\eta_t=\eta\), we expect to converge to an approximate critical point in \(O\pa{ d\epsilon^{-4} }\) as long as \(\eta\simeq\min\pa{L^{-1},\epsilon^2}\). With annealing, \(\eta_t\simeq\min(L^{-1},\epsilon t^{-1/4})\) offers the same guarantees.

Practical Notes. Vanilla SGD, though simple, has quite a few pitfalls without careful tuning.

• Its theoretical performance is poor, and convergence is only guaranteed to hold if assuming step size is kept small corresponding to smoothness constants of the cost function. The fact that annealing doesn’t benefit worst-case runtime is a bit surprising since that’s what happens in the strongly convex case, but I believe this is a testament to the fact that the general cost function shape is no longer bowl-like, but can be fractal in nature, so there might never be an end to directions to descend.
• In practice, I’ve found that at least for simple problems like logistic regression, where we have \(L\) available, using a fixed learning rate of at most \(L^{-1}\), is many, many orders of magnitudes slower than a “reasonable” constant. Global Lipschitz properties might be poorer than local ones, so you’re dooming yourself to slow learning.
• A common strategy to cope with this is to use an exponential decay schedule, \(\eta_t\simeq e^{-t}\), with the idea being to traverse a large range of learning rates, hopefully spending most of the time in a range appropriate to the problem. Of course, this will be very sensitive to hyper parameters: note that using exponential decay bounds the diameter of exploration, and even using an inverse-time schedule \(\eta_t\simeq t^{-1}\) for \(T\) steps means you can only travel \(O(\log T)\) distance from your starting point! Inverse-time schedules, and more generally schedules with \(\sum_{t=1}^\infty\eta_t=\infty\) but \(\sum_{t=1}^\infty\eta_t^2<\infty\), can draw on more restrictive smoothness assumptions about \(f\) to guarantee almost-sure convergence (Bottou 1998).
• Ghadimi and Lan 2013a also offer a treatment of “2-phase random stochastic gradient”, which is vanilla SGD with random restarts, for probabilistic guarantees of finding approximate stationary points. Finally, Ghadimi and Lan’s SGD technically expects to find \(\vx_*\) with \(\E\ha{\norm{\nabla f(\vx_*)}^2}<\epsilon\). This implies the above \(O(d\epsilon^{-4})\) convergence rate, but is technically slightly stronger.

Most subsequent algorithms have been developed to handle finding \(\eta_t\) on their own, adapting the learning rate as they go along. This was done for the convex case, but that doesn’t stop us from applying the same improvements to the non-convex case!

Accelerated (Stochastic) Gradient Descent (AGD)

See tf.train.MomentumOptimizer for implementation. AGD is motivated by momentum-added SGD from Polyak 1964. A modern version looks like this: \[ \begin{align} \vm_0&=0\\\
\vm_{t+1}&=\beta \vm_t+\eta \nabla_t \\\
\vx_{t+1}&=\vx_t-\vm_{t+1} \end{align} \] Description. We can intuit this as, in Ruder’s words, as a ball rolling down a hill, with a growing momentum. In this way, we extend the hill metaphor, in effect trusting that we can continue further in the general downhill direction maintained by the momentum terms. Some momentum implementations just replace the above gradient with the estimator \(\tilde{\nabla}_t\) and set stuff running, like the linked TensorFlow optimizer does by default. However, even with full gradient information and assuming smoothness and convexity, momentum alone doesn’t perform optimally. Nesterov’s 1983 paper, A method of solving a convex programming problem with convergence rate \(O(1/k^2)\), fixes this by correcting momentum to look ahead, which is helpful if the curvature of the function starts changing: \[ \begin{align} \vm_0&=0\\\
\vm_{t+1}&=\beta \vm_t+\eta \nabla f(\vx_t -\beta\vm_t)\\\
\vx_{t+1}&=\vx_t-\vm_{t+1} \end{align} \] Practical Notes. While optimal in the smooth, convex, full gradient setting, and even optimally extended to non-smooth settings (see Tseng 2008 for an overview), changing the above to use a random gradient estimator ruins asymptotic performance, concede Sutskever et al 2013. Goodfellow claims momentum handles ill-conditioning in the Hessian of \(f\) and variance in the gradient though the introduction of the stabilizing term \(\vm_{t}\). Indeed, this seems to be the thesis laid out by Sutskever et al 2013, where the authors argue that a certain transient phase of optimization matters more for deep NNs, which AGD accelerates empirically (see also Bengio et al 2012). Many authors set \(\beta=0.9\), but see Sutskever et al 2013 for detailed considerations on the momentum schedule.

Guarantees. Later work by Ghadimi and Lan 2013b solidifies the analysis for AGD in for stochastic, smooth, composite, and non-convex costs, though it uses a slightly different formulation for momentum. Under the previous gradient estimation assumptions from SGD (including slightly stronger light-tail assumptions about the variance of \(\tilde{\nabla}_t\)), \(L\)-gradient-Lipschitz assumptions for \(f\), and a schedule which increases mini-batch size linearly in the iteration count to refine gradient estimation, AGD requires \(O(\epsilon^{-2})\) iterations but \(O(d\epsilon^{-4})\) runtime to converge to an approximate critical point. Perhaps with yet stronger assumptions about the concentration of \(\tilde{\nabla}_t\) around \(\nabla_t\) AGD has promise to perform better.

AdaGrad

AdaGrad was proposed by Duchi et al 2011 and is available in TensorFlow. \[ \begin{align} \vv_0&=\epsilon\\\
\vv_{t+1}&=\vv_t+\tilde{\nabla}_t^2\\\
\vx_{t+1}&=\vx-\frac{\eta}{\sqrt{\vv_{t+1}} }\tilde{\nabla}_t \end{align} \] Description. AdaGrad is actually analyzed in the framework of online convex optimization (OCO). This adversarial, rather than stochastic, optimization setting can immediately be applied to stochastic optimization of convex functions over compact sets. The first is based on OCO. Consider an \(L\)-gradient Lipschitz but possibly nonconvex cost \(f\) at some iterate \(\vx_t\), which implies an upper bound \(f(\vx)\le f(\vx_t)+(\vx-\vx_t)^\top\nabla_t+\frac{L}{2}\norm{\vx-\vx_t}^2_2\); the convexity inequality, if we had it, would sandwich \(f(\vx)\ge f(\vx_t)+(\vx-\vx_t)^\top\nabla_t\). Minimizing this upper bound, which results in full gradient descent (GD), then, guarantees improvement in our cost. The quadratic term effectively quantifies how much we trust our linear approximation. An analogous technique applied to a sequence of cost functions in the online setting gives rise to Follow the Regularized Leader (FTRL): given past performance, create an upper bound on the global cost reconstructed from our stochastic information, and find the next best iterate subject to working within a trusted region. The difficulty is in defining this trusted region with an unfortunately named regularization function, which differs from \(\Omega\). AdaGrad improves the quadratic regularization \(\frac{L}{2}\norm{\vx-\vx_t}^2_I\) in GD to the less crude \(\frac{L}{2}\norm{\vx-\vx_t}^2_{G_t}\), where \(\norm{\vx}^2_A=\vx^\top A\vx\) and \(G_t=\diag \vv_t^{1/2}\) from the iterates above (see these notes, retrieved from here, for discussion). This adaptive regularization function, at least in the OCO setting, is as good, in terms of convergence, as an optimal choice quadratic regularization, up to multiplicative constants. We see that the learning rate for every feature changes with respect to its history, so that new information is weighed against the old.

Practical Notes. AdaGrad is a convex optimization algorithm, and it shows, but not in a good way.

• In nonconvex optimization problems, aggregates of gradients from the beginning of training are irrelevant to the curvature of the current location being optimized, Goodfellow claims. As a result, they result in aggressive learning rate decrease.
• The \(\epsilon\) constant is only for numerical stability. Keras and Ruder recommend setting it to \(10^{-8}\).
• For noncomposite versions of AdaGrad, see tf.train.AdagradDAOptimizer, mentioned in the original Duchi et al 2011 and tf.train.ProximalAdagradOptimizer based on FOBOS from Duchi et al 2009. See McMahan 2011 for discussion.
• While AdaGrad greatly improved performance by having a per-dimension learning rate, its use is frequently discouraged because of its maintenance of the entire gradient history.

AdaDelta attempts to address the aggressive learning rate decrease problem of AdaGrad by exponentially decaying an estimate of accumulated gradient term \(\vv_t\) (Zeiler 2012). This adds a new parameter for the exponential decay \(\beta\), typically \(0.9\), and introduces a unit correction \(\tilde{\vx}_t\) in place of the learning rate: \[ \begin{align} \vv_0&=\tilde{\vx}_0=0\\\
\vv_{t+1}&=\beta \vv_t+(1-\beta)\tilde{\nabla}_t^2\\\
\Delta_{t+1}&=\frac{\sqrt{\tilde{\vx}_{t}+\epsilon} }{\sqrt{\vv_{t+1}+\epsilon} }\tilde{\nabla}_t\\\
\tilde{\vx}_{t+1}&=\beta \tilde{\vx}_{t}+(1-\beta)\Delta_{t+1}\\\
\vx_{t+1}&=\vx_t-\Delta_{t+1} \end{align} \] Similar update rules have been explored by Schaul et al 2012 in a sound but presumptive setting where \(\nabla^2f_i(\vx)\) are considered identical and diagonal for all \(i\in[n]\) and any fixed \(\vx\). RMSProp is similar to AdaDelta, but still relies on a fixed learning rate \(\tilde{\vx}_t=\eta\). Both RMSProp and AdaDelta have seen practical success, improving over AdaGrad in later iterations because they are unencumbered by previous gradient accumulation. RMSProp even has a Nesterov momentum variant. However, the exponential decay approximation may have high bias early in the iteration. The Adaptive Moment Estimation (Adam) paper corrects for this.

Adam

The Adam method, proposed by Kingma and Ba 2014, improves on AdaGrad-inspired adaptive rate methods by adding both a momentum term and removing first and second moment bias from exponential decay approximations to the gradient accumulators. See TensorFlow for an implementation. \[ \begin{align} \vm_0&=\vv_0=0\\\
\vm_{t+1}&=\beta_1\vm_t+(1-\beta_1)\tilde{\nabla}_t \\\
\vv_{t+1}&=\beta_2 \vv_t+(1-\beta_2)\tilde{\nabla}_t^2\\\
\vx_{t+1}&=\vx_t-\eta\pa{1-\beta_2^t}^{1/2}\pa{1-\beta_1^t}^{-1}\frac{\vm_{t+1} }{\sqrt{\vv_{t+1}+\epsilon} } \end{align} \] Description. Adam seeks to combine AdaGrad’s adapitivity, which can learn the curvature of the space it’s optimizing in (making it able to deal with sparse gradients), and momentum-based approaches like RMSProp, which are able to adapt to new settings during the course of the optimization. The bias correction ensures that, roughly, \(\E\ha{ \tilde{\nabla}_t^2} =\vv_t(1-\beta_2^t)+\zeta\) and analogously for \(\vm_t\), with \(\zeta\) being the error that occurs from non-stationarity in the gradient. Under the assumption that appropriate \(\beta_1,\beta_2\) are selected, such that the non-stationarity error is appropriately vanished by the exponential decay, Adam has low bias for the gradient moments \(\vm,\vv\). As the paper describes, the unbiased \(\frac{\vm_{t+1} }{\sqrt{\vv_{t+1}+\epsilon} }\) captures the signal-to-noise ratio for the gradient.

Guarantees. Adam reduces to Adagrad under certain parameter settings. Like Adagrad, it has strong guarantees in an OCO setting, which are valuable but not immediately applicable here.

Practical Notes. Given that Adam has fairly intuitive hyperparameters, Adam has pretty decent performance across the board.

• As before, for stability, a small \(\epsilon=10^{-8}\) is typically used.
• AdaGrad can be recovered with an annealing \(\eta\sim t^{-1/2}\) and near-0 values for\(\beta_1, 1-\beta_2\): these are recommended in the convex setting.
• For other, nonconvex, settings \(\beta_1\) should be higher, for instance, \(0.9\). Settings for \(\beta_2\) from the paper are among \({0.99, 0.999,0.9999}\). High settings for both \(\beta_1,\beta_2\) imply stationarity in the gradient moments.
• Though Adam and other adaptive methods might seem like empirical improvements over SGD (though they certainly don’t seem to have any better convergence guarantees in the nonconvex case), they seem to struggle with generalization error, which is the ultimate goal for our optimization. Recall the point made in the overview post about Bousquet and Bottou 2007: the convergence guarantees for the training loss above are only part of the overall error equation. This is still an active area of research, but intuitively we can construct training sets where adaptive methods reach poorly generalizing minima but SGD methods approach well-generalizing good ones (Wilson et al 2017). Empirical responses to this have found that momentum-based SGD can be tuned to address the convergence speed issues but avoid generalization error qualms (Zhang et al 2017). I would posit that SGD perhaps finds “stable” minima (ones whose generalization gap is small, conceptually minima that exist on a large, flat basin), and that momentum does not affect this approach, whereas adaptive methods might find a minimum within a narrow valley that might have better training loss, but has a large generalization gap since the valley “feature” of this cost function terrain is unstable with respect to the training set.

Visualization

This visualization is coming from Sebastian Ruder’s related post. Check it out for discussion about the below visualization. Note that NAG is AGD and Momentum is uncorrected momentum added to SGD.

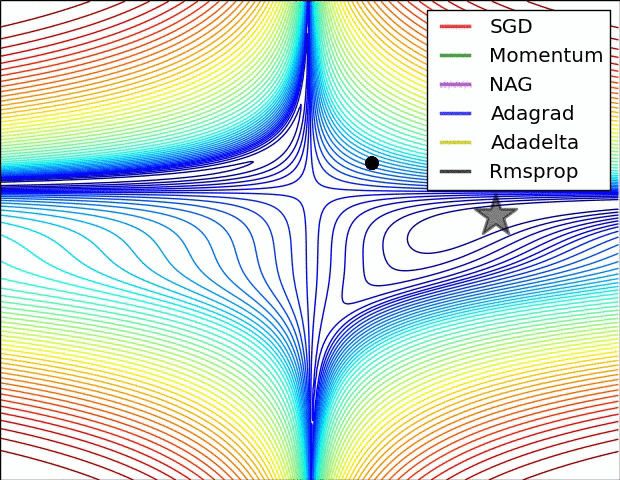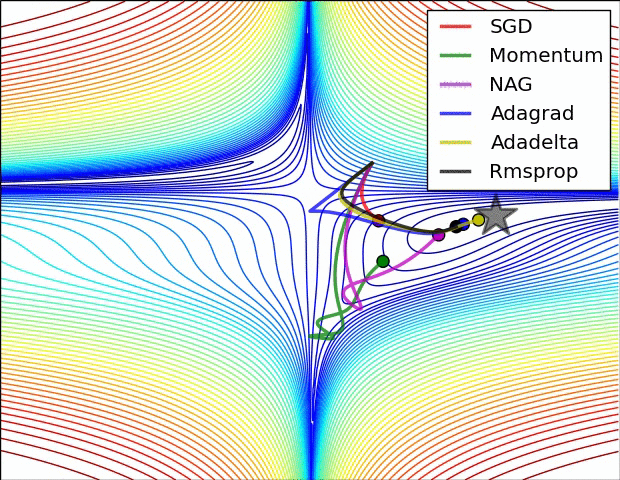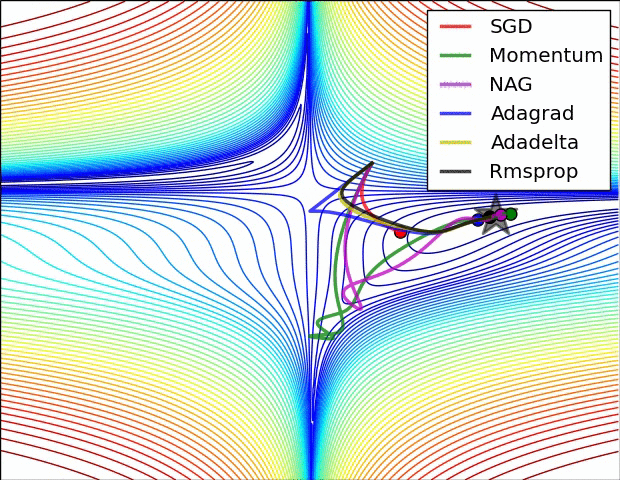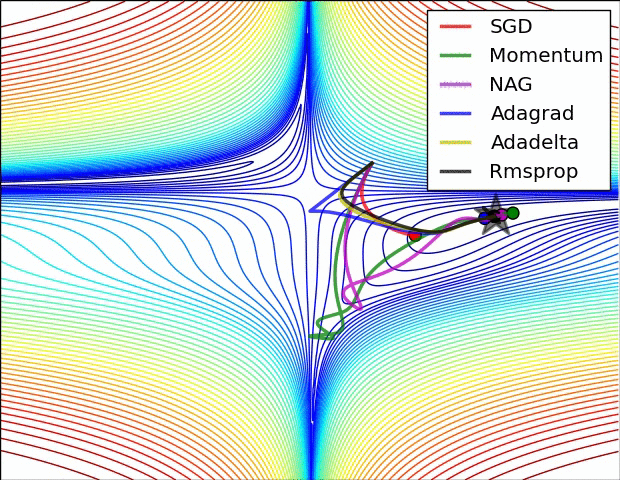
Future Directions

Variance Reduction

A new approach, Stochastic Variance Reduction Gradient (SVRG), was developed by Johnson and Zhang 2013. Its analysis, for strongly convex and smooth non-composite functions, didn’t improve any long-standing convergence rates, but the idea introduced was novel: we could use stale full-gradient information \(\nabla_t\) taken occasionally to de-noise stochastic estimations \(\tilde{\nabla}_t\). Updating our full gradient every \(m\) steps, with \(\tilde{\nabla}_t(\vx)\) being the stochastic estimator for the cost gradient at time \(t\) at location \(\vx\), so the previous defualt notation has \(\tilde{\nabla}_t=\tilde{\nabla}_t(\vx_t)\): \[ \begin{align} \bar{\vx}_t &= \begin{cases}\E_{\xi}\bar{\vx}_{t-\xi}& t\equiv 0\pmod{m} \\\\ \bar{\vx}_{t-1} & \text{otherwise}\end{cases} \\\
\vg_t &= \begin{cases} \nabla f(\bar{\vx}_t) & t\equiv 0\pmod{m} \\\\ {\vg}_{t-1} & \text{otherwise}\end{cases} \\\
\vx_t &= \vx_{t-1}- \eta_t\pa{\tilde{\nabla}_t (\vx_{t-1})-\tilde{\nabla}_t(\bar{\vx}_{t})+\vg_t} \end{align} \] Above, \(\xi\) is a random variable supported on \([m]\). The same guarantees hold without taking expectation wrt \(\xi\) for computing \(\bar{\vx}_t\). In particular, for certain \(\xi,\eta_t\) SVRG was shown to reach an approximate critical points in \(O(dn+dn^{2/3}\epsilon^{-2})\) time, at least in the non-composite setting, simultaneously by Reddi et al 2016 and Allen-Zhu and Hazan 2016. For these problems this improves over the GD runtime cost \(O(dn\epsilon^{-2})\).

Still, it’s debatable whether the \(O(d\epsilon^{-4})\) SGD is improved upon by SVRG methods, since they depend on \(n\). Datasets can be extremely large, so the \(n^{2/3}\epsilon^{-2}\) term may be prohibitive. At least in convex settings, Babanezhad et al 2015 explore using mini-batches for a variance-reduction effect. Perhaps an extension of this to non-convex costs would be what’s necessary to see SVRG applied to NNs. Right now, its use doesn’t seem to be very standard.

Noise-injected SGD

Noisy SGD, is a surprisingly cheap and viable new solution proposed to find approximate local minima by Ge et al 2015. Intuitively, adding jitter the parameters would ensure that the gradient-vanishing pathology of strict saddle points won’t be a problem. In particular, even if the gradient shrinks as you near a saddle point, the jitter will be strong enough that you won’t have to spend a long time around it before escaping.

\[ \begin{align} \xi_{t}&\sim \Uniform \pa{B_{1} }\\\
\vx_{t+1}&=\vx_t-\eta \tilde{\nabla_{t} }+\xi_t \end{align} \]

Above, \(B_r\) is a ball centered at the origin of radius \(r\). Unfortunately, noisy SGD is merely \(O(\poly(d/\epsilon))\). Its important contribution is showing that even stochastic first order methods could feasibly be used to arrive at local minima. With additional assumptions, and removing stochasticity, this was improved by Jin et al 2017 in Perturbed Gradient Descent (PGD): \[ \begin{align} \xi_{t}&\sim \Uniform \pa{B_{r_t} }\\\
\vx_{t+1}&=\vx_t-\eta \nabla_{t}+\xi_t \end{align} \] The radius \(r_t\) is carefully chosen depending on whether or not PGD detects we are near a saddle point. Usually, it is set to 0, so the algorithm mostly behaves like GD. With some additional second-order smoothness assumptions, this runs in time \(O(nd\epsilon^{-2}\log^4d)\), showing a cheap extension of GD for finding minima. However, until a similar analysis is performed for stochastic PGD, with equally friendly results, these methods aren’t yet ready for prime time. Recent work by Chi Jin adds acceleration to PGD, improving by a factor of \(\epsilon^{1/4}\).