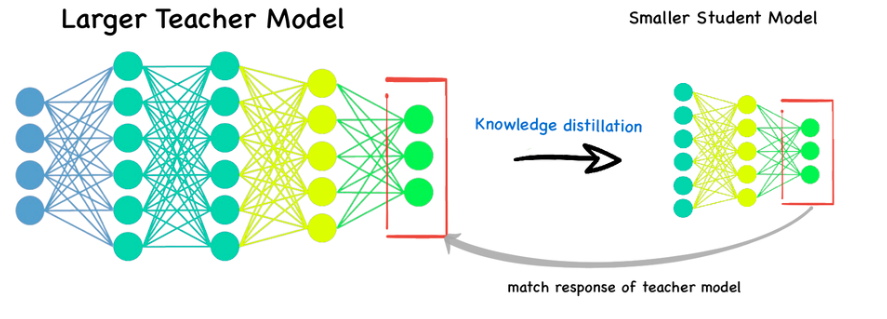
Distillation Walkthrough Distillation is a critical technique towards improving a network’s quality while keeping its serving latency constant. This is becoming crucial as people focus on serving larger and larger models. Image found on LinkedIn. Distillation is a powerful technique, but a couple things about it are quite mystical. The purpose of this post is to: Provide a very high level explainer (but mostly refer to source papers) of distillation. Show that you can create a simp... Read More

Introduction In this blog post, I’ll provide data stream background, applied context, motivation, and an overview for my recent work, Sketchy, co-authored with Xinyi Chen, Y. Jennifer Sun, Rohan Anil, and Elad Hazan, which will be featured in NeurIPS 2023 proceedings. I really enjoyed working on this project because it simultaneously scratches different methodological itches of mine, from data stream sketching to online convex optimization. However, the algorithm introduced here was borne o... Read More

A serpentine wall, or crinkle crankle wall, may seem like a surprising structure to use for fences, but may end up being more efficient in terms of building material than a straight fence which must withstand the same horizontal forces. In a post which is the raison d’etre for this one, John D. Cook derives a formula for computing the arc length of a sinusoidal curve. By assuming that such a sinusoidally-shaped wall could withstand lateral forces as much as a straight wall would, had the s... Read More

This post is not like my usual posts. Over the last two weeks, I went on a Birthright trip to Israel. It was an uncharacteristically spiritual journey for me. I was agnostic as a child. But this didn’t get in the way of my Jewish self-definition. Early on, I heard stories from my grandpa about his grandma’s execution by the Einsatzgruppen. In my ancestor’s deaths was a conviction for my own identity. My group visited Yad Vashem a few days into the trip. I didn’t expect to learn anything ... Read More

I’ve added heavy hitters functionality to the dsrs crate (in addition to a variant of Count-Min). It’s another streaming algorithm which helps us find the most popular repeated lines in a stream. In this blog post, we’ll see how this approximate algorithm saves memory over an exact approach. For instance, maybe we have access logs which contain IP addresses like so: 1.1.1.1 3.1.2.3 1.1.1.1 4.2.1.2 1.1.1.1 where there could be millions of unique IP addresses accessing our server, but we’d ... Read More

The VLAD (vector of locally aggregated descriptors) (no relation!) algorithm was proposed as a mechanism for compacting image descriptors (related follow-on work). This is useful for creating similarity search indices. A reader of my blog referred me to this algorithm, noting that the supposedly vectorized version turns out slower than non-vectorized code. We review indexing and broadcasting rules to diagnose the slowdown and prescribe a fix with a lesser-known numpy gem for what’s known as ... Read More

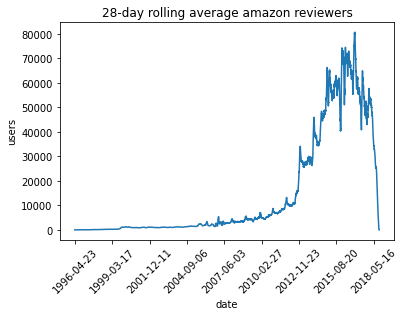
To show off a recent command line tool for sketching, dsrs, let’s plot the rolling 28-day average daily count of active reviewers on Amazon. The raw data here is item,user,rating,timestamp so this would map to a sophisticated GROUP BY with a COUNT DISTINCT over 28-day windows in SQL. But since the data’s only available as CSV, how can we get to the same answer? If we’re just interested in an approximate solution, can we do this without using a bunch of memory or custom (shuffle-inducing…) sl... Read More

Step aside, map reduce. In this post, I’ll introduce a single-machine utility for parallel processing that significantly improves upon the typical map-reduce approach. When dealing with GB-to-TB size datasets, using a large multiprocessing machine should be enough for fast computation, but performance falls short of expectations due to naive reduce implementations. Let’s take the canonical map reduce example, word count, where our goal is to take a corpus of text and construct a map from wor... Read More

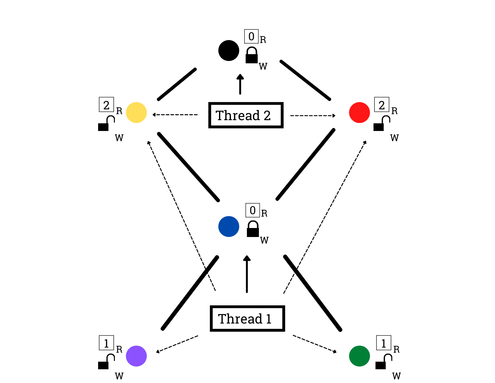
Markov Chain Monte Carlo methods (MCMC) are, functionally, very cool: they enable us to convert a specification of a probability distribution from a likelihood \(\ell\) into samples from that likelihood. The main downside is that they’re very slow. That’s why lots of effort has been invested in data-parallel MCMC (e.g., EPMCMC). This blog post takes a look at a specialized MCMC sampler which is transition-parallel, for a simple distribution: Given a fixed, simple, large graph \(G=(V,E)\) ... Read More

Lots of sparse datasets are kept around in a convenient text format called SVMlight. It’s easy to manipulate with unix tools and very easily compressed so it’s perfect to distribute. However, the main way that’s available to access this format in python is dreadfully slow due to a natural lack of parallelism. svm2csr is a quick python package I wrote with a rust extension that parallelizes SVMlight parsing for faster loads in python. Check it out! P.S., here’s what this format looks like: ... Read More

Frequently, we run into situations where we need to deal with arrays of varying sizes in numpy. These result in much slower code that deals with different sizes individually. Luckily, by extracting commutative and associative operations, we can vectorize even in such scenarios, resulting in significant speed improvements. This is especially pronounced when doing the same thing with deep learning packages like torch, because vectorization matters a lot more on a GPU. For instance, take a typi... Read More

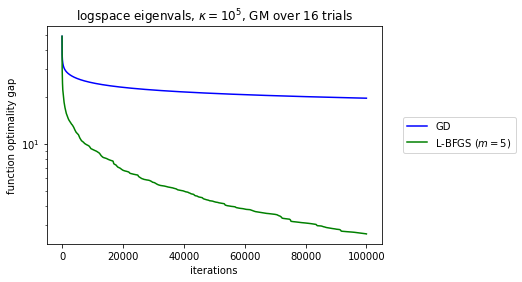
Curiously, the original L-BFGS convergence proof essentially reduces the L-BFGS iteration to GD. This establishes L-BFGS converges globally for sufficiently regular functions and also that it has local linear convergence, just like GD, for smooth and strongly convex functions. But if you look carefully at the proof, the construction is very strange: the more memory L-BFGS uses the less it looks like GD, the worse the smoothness constants are for the actual local rate of convergence. I go to ... Read More

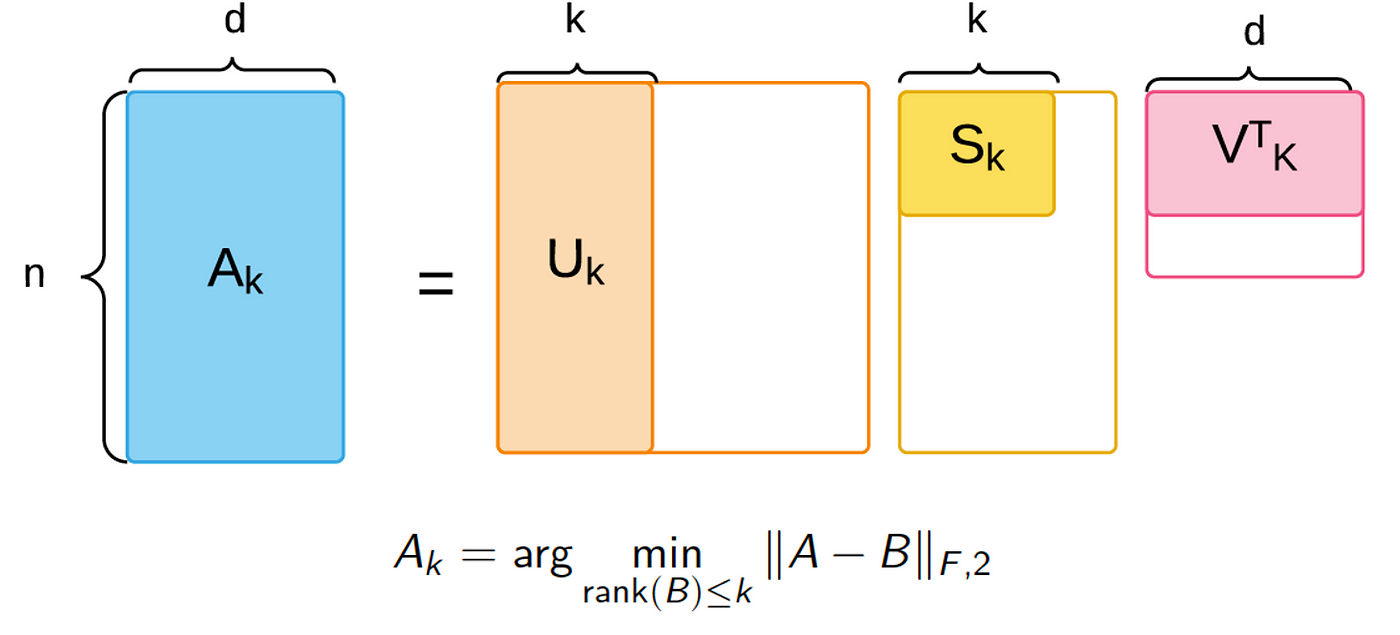
This notebook comes from my Linear Regression Analysis notes. In the ordinary least squares setting, we model our outputs \(\mathbf{y}=X\boldsymbol\beta+\boldsymbol\varepsilon \) where \(\boldsymbol\varepsilon\sim N(\mathbf{0}, \sigma^2 I) \), with \(\boldsymbol\beta,\sigma^2 \) unknown. As a result the OLS fit \(\hat{\boldsymbol\beta}\sim N\left((X^\top X)^{-1}X^\top \mathbf{y},\sigma^2 (X^\top X)^{-1}\right) \) (an distribution with an unknown variance scaling factor which we must sti... Read More

I just finished up reading Linear Regression Analysis by George Seber and Alan Lee. I really enjoyed it. Requisite Background I came in with some background in theoretical statistics (Keener and van der Vaart), and that really enriched the experience. That said, the first two chapters establish necessary statistical pre-requisites, so it seems like the main prerequisite to understand the book is mathematical maturity (calculus, linear algebra, elementary probability). Style The book is fa... Read More

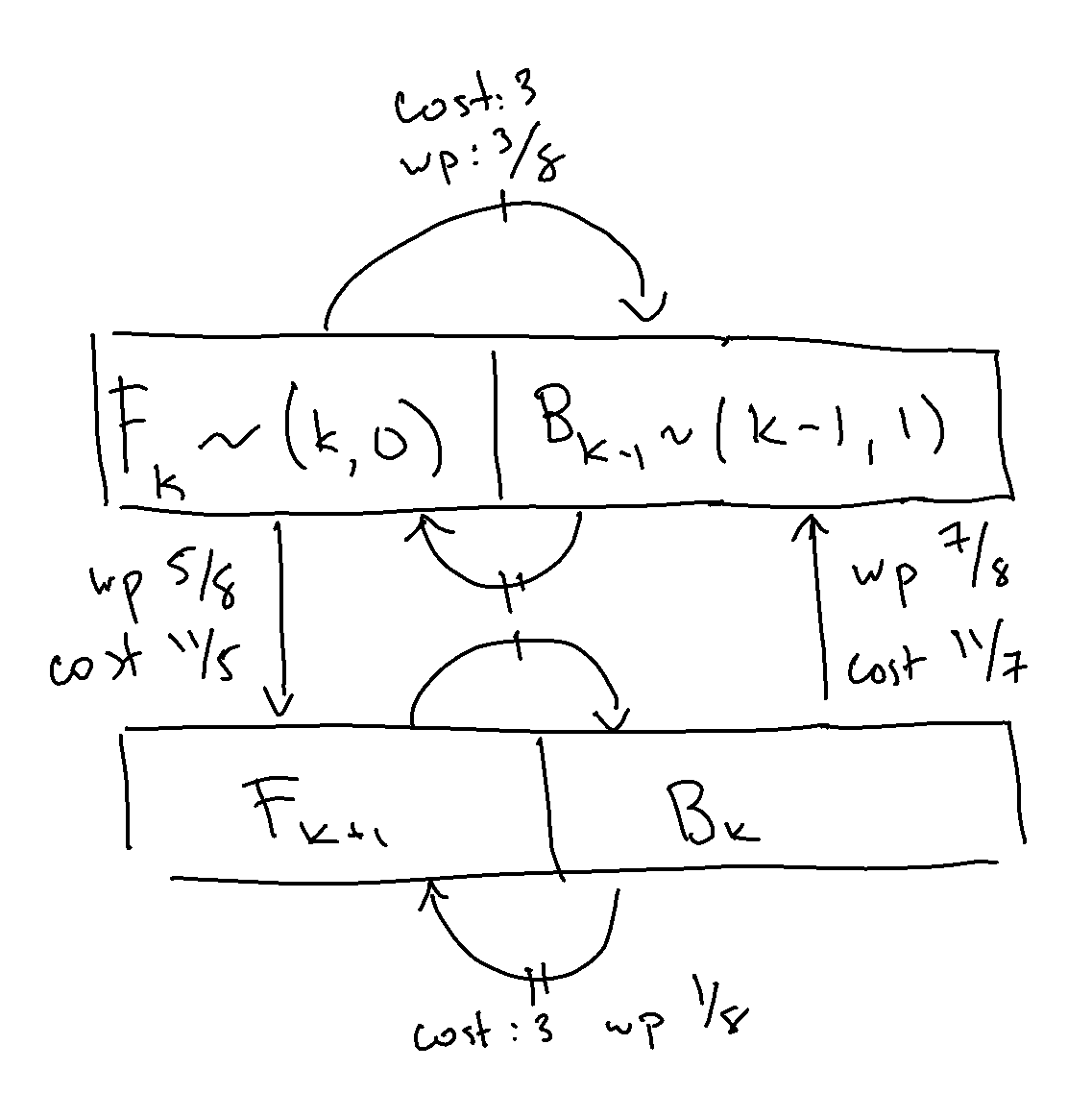
Last time, we discussed the RCT2 problem, which we won’t delve into in great detail, but at a high level, we have an inductively defined Markov chain, parameterized by \(n \), with special start and end states and the following outgoing arrows, such that for \(k\in[n] \), we have the following transition dynamics: from IPython.display import Image Image(filename='transitions.png') We already went over how to solve the expected hitting time for the end state for a given, known \(n \).... Read More

Roller Coaster Tycoon 2 (RCT2) Problem In Roller Coaster Tycoon 2, you play as the owner of an amusement park, building rides to attract guests. One ride you can build is a maze. It turns out that, for visual appeal, guests traverse mazes using a stochastic algorithm. Marcel Vos made an entertaining video describing the algorithm, which has in turn spawned an HN thread and Math SE post. I really enjoyed solving the problem and wanted to share the answer as well as some further thoughts. M... Read More

In the previous post, we discussed a particular quantity, \(\mathbb{P}\{X=1\} \), where \(X \) follows a Poisson Binomial distribution, parameterized by \(\{p_j\}_{j=1}^n \). This means that \(X=\sum_jX_j \), where \(X_j \) are Bernoulli- \(p_j \) independent random variables. We came up with an \(O(1) \) memory and \(O(n) \) time approach to computing the desired probability, and gave an example where even the best approximations can be poor. What about a more general question? Let’... Read More

This article investigates a fun thought experiment about the Poisson-Binomial distribution. Let’s imagine we’re designing a large hash table. We know up-front we’re going to get \(n \) distinct keys, so let’s number them \(j\in [n] \). Ahead of time, we’re allowed to see the set of hashes the \(j \)-th key will belong to. It is allowed to take on one of \(c_j \) distinct hashes, \(S_j=\{h_1, \cdots, h_{c_j}\}\subset\mathbb{N} \), where at run time the real hash is sampled uniformly (an... Read More

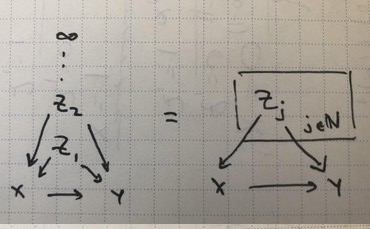
One neat takeaway from the previous post was really around the structure of what we were doing. What did it take for the infinite DAG we were building to become a valid probability distribution? We can throw some things out there that were necessary for its construction. The infinite graph needed to be a DAG We needed inductive “construction rules” $\alpha,\beta$ where we could derive conditional kernels from a finite subset of infinite parents to a larger subset of the infinite paren... Read More

This is Problem 9.11 in Elements of Causal Inference. _Construct a single Bayesian network on binary $X,Y$ and variables $\{Z_j\}_{j=1}^\infty$ where the difference in conditional expectation, \[\begin{align} \Delta_j(\vz_{\le j}) &=\\ & \CE{Y}{X=1, Z_{\le j}=\vz_{\le j}}-\\ & \CE{Y}{X=0, Z_{\le j}=\vz_{\le j}}\,\,, \end{align}\] satisfies $\DeclareMathOperator\sgn{sgn}\sgn \Delta_j=(-1)^{j}$ and $\abs{\Delta_j}\ge \epsilon_j$ for some fixed $\epsilon_j>0$. $\Delta_0$ is unc... Read More