$$ \newcommand{\bsth}{{\boldsymbol\theta}} \newcommand{\nptime}{\textsf{NP}} \newcommand{\ptime}{\textsf{P}} \newcommand{\disteq}{\overset{d}{=}} %linalg \newcommand{\mat}[1]{\begin{pmatrix} #1 \end{pmatrix}} \newcommand{\detmat}[1]{\begin{vmatrix} #1 \end{vmatrix}} \newcommand{\spanb}[1]{\text{span}\{ #1 \}} \DeclareMathOperator{\conv}{conv} % convex hull \DeclareMathOperator{\cone}{cone} \DeclareMathOperator{\vectorize}{vec} \DeclareMathOperator{\matricize}{mat} \DeclareMathOperator{\adj}{adj} \DeclareMathOperator{\diag}{diag} \DeclareMathOperator{\tr}{tr} \DeclareMathOperator{\rank}{rank} \DeclareMathOperator*{\argmin}{argmin} \DeclareMathOperator*{\proj}{proj} % brackets, norms, cardinalities \newcommand{\pa}[1]{ \left({#1}\right) } \newcommand{\ha}[1]{ \left[{#1}\right] } \newcommand{\ca}[1]{ \left\{{#1}\right\} } \newcommand{\inner}[1]{\left\langle #1 \right\rangle} \newcommand{\innercpy}[1]{\inner{ #1, #1 }} \newcommand{\norm}[1]{\left\| #1 \right\|} \newcommand{\abs}[1]{\left|{#1}\right|} \newcommand{\card}[1]{\left\vert{#1}\right\vert} % math vectors \newcommand{\va}{\textbf{a}} \newcommand{\vb}{\textbf{b}} \newcommand{\vc}{\textbf{c}} \newcommand{\vd}{\textbf{d}} \newcommand{\ve}{\textbf{e}} \newcommand{\vf}{\textbf{f}} \newcommand{\vg}{\textbf{g}} \newcommand{\vh}{\textbf{h}} \newcommand{\vi}{\textbf{i}} \newcommand{\vj}{\textbf{j}} \newcommand{\vk}{\textbf{k}} \newcommand{\vl}{\textbf{l}} \newcommand{\vm}{\textbf{m}} \newcommand{\vn}{\textbf{n}} \newcommand{\vo}{\textbf{o}} \newcommand{\vp}{\textbf{p}} \newcommand{\vq}{\textbf{q}} \newcommand{\vr}{\textbf{r}} \newcommand{\vs}{\textbf{s}} \newcommand{\vt}{\textbf{t}} \newcommand{\vu}{\textbf{u}} \newcommand{\vv}{\textbf{v}} \newcommand{\vw}{\textbf{w}} \newcommand{\vx}{\textbf{x}} \newcommand{\vy}{\textbf{y}} \newcommand{\vz}{\textbf{z}} \newcommand{\vzero}{\textbf{0}} \newcommand{\vone}{\textbf{1}} \newcommand{\valpha}{{\boldsymbol\alpha}} \newcommand{\vepsilon}{{\boldsymbol\epsilon}} \newcommand{\vnu}{{\boldsymbol\nu}} \newcommand{\vpi}{{\boldsymbol\pi}} \newcommand{\veta}{{\boldsymbol\eta}} \newcommand{\vsigma}{ {\boldsymbol\sigma}} \newcommand{\vbeta}{ {\boldsymbol\beta}} \newcommand{\vtheta}{ {\boldsymbol\theta}} \newcommand{\vdelta}{ {\boldsymbol\delta}} \newcommand{\vlambda}{ {\boldsymbol\lambda}} \newcommand{\vmu}{ {\boldsymbol\mu}} % common math sets \newcommand{\Z}{\mathbb{Z}} \newcommand{\R}{\mathbb{R}} \newcommand{\C}{\mathbb{C}} \newcommand{\N}{\mathbb{N}} \newcommand{\Q}{\mathbb{Q}} \newcommand{\F}{\mathbb{F}} \newcommand{\T}{\mathbb{T}} % limits \def\sumn{\sum_{n=0}^\infty} \def\limn{\lim_{n\rightarrow\infty}} \def\prodn{\prod_{n=0}^\infty} % mathcal \newcommand{\mcA}{\mathcal{A}} \newcommand{\mcB}{\mathcal{B}} \newcommand{\mcC}{\mathcal{C}} \newcommand{\mcD}{\mathcal{D}} \newcommand{\mcE}{\mathcal{E}} \newcommand{\mcF}{\mathcal{F}} \newcommand{\mcG}{\mathcal{G}} \newcommand{\mcH}{\mathcal{H}} \newcommand{\mcI}{\mathcal{I}} \newcommand{\mcJ}{\mathcal{J}} \newcommand{\mcK}{\mathcal{K}} \newcommand{\mcL}{\mathcal{L}} \newcommand{\mcM}{\mathcal{M}} \newcommand{\mcN}{\mathcal{N}} \newcommand{\mcO}{\mathcal{O}} \newcommand{\mcP}{\mathcal{P}} \newcommand{\mcQ}{\mathcal{Q}} \newcommand{\mcR}{\mathcal{R}} \newcommand{\mcS}{\mathcal{S}} \newcommand{\mcT}{\mathcal{T}} \newcommand{\mcU}{\mathcal{U}} \newcommand{\mcV}{\mathcal{V}} \newcommand{\mcW}{\mathcal{W}} \newcommand{\mcX}{\mathcal{X}} \newcommand{\mcY}{\mathcal{Y}} \newcommand{\mcZ}{\mathcal{Z}} % distribs, probability \newcommand{\disteq}{\overset{d}{=}} \newcommand\independent{\perp \!\!\! \perp} \DeclareMathOperator{\Laplace}{Laplace} \DeclareMathOperator{\Poisson}{Poisson} \DeclareMathOperator{\Exponential}{Exponential} \DeclareMathOperator{\Multinomial}{Multinomial} \DeclareMathOperator{\Bernoulli}{Bernoulli} \DeclareMathOperator{\Categorical}{Categorical} \DeclareMathOperator{\Uniform}{Uniform} \DeclareMathOperator{\Binomial}{Binomial} \DeclareMathOperator{\Hypergeometric}{Hypergeometric} \DeclareMathOperator{\GammaDist}{Gamma} \DeclareMathOperator{\NegativeBinomial}{NegativeBinomial} \DeclareMathOperator\sub{sub} \renewcommand{\d}[1]{\mathop{\mathrm{d} #1 }} \newcommand{\dkl}[2]{\mathop{D_\mathrm{KL}}\left({#1}\;\middle\|\;{#2}\right)} \newcommand{\sg}{\mathop{\mathrm{SG}}} \newcommand{\se}{\mathop{\mathrm{SE}}} %operators \DeclareMathOperator{\power}{{\mathcal{P}}} \DeclareMathOperator{\var}{var} \DeclareMathOperator{\cov}{cov} \DeclareMathOperator\mathProb{\mathbb{P}} \DeclareMathOperator\mathExp{\mathbb{E}} \DeclareMathOperator*\mathExpUnder{\mathbb{E}} \DeclareMathOperator*\fat{fat} \renewcommand{\P}{\mathProb} % need to overwrite stupid paragraph symbol \newcommand{\E}{\mathExp} % need to overwrite stupid paragraph symbol \newcommand{\set}[2]{ \left\{ #1 \,\middle|\, #2 \right\} } \newcommand{\CE}[2]{ \mathExp\left[ #1 \,\middle|\, #2 \right] } \renewcommand{\CP}[2]{ \mathProb\left\{ #1 \,\middle|\, #2 \right\} } $$

Articles by category: optimization

---

graph-processing parallel distributed-systems online-learning machine-learning my-whitepapers hardware-acceleration interview-question tools optimization deep-learning numpy-gems joke-post philosophy causal statistics numpy tricks history llm pretraining

---

Distillation Walkthrough

04 Feb 2024

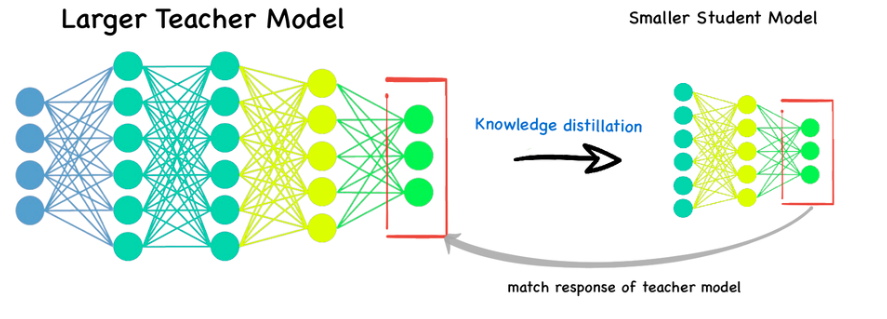
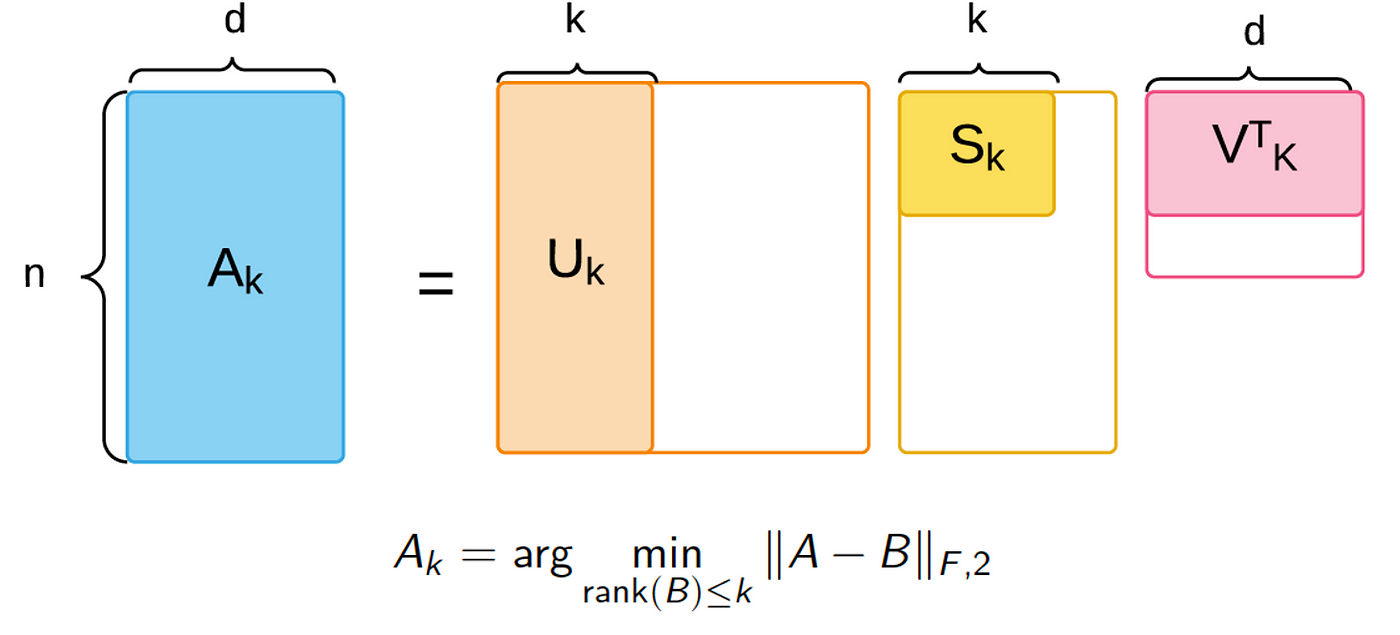
Distillation WalkthroughDistillation is a critical technique towards improving a network’s quality while keeping its serving latency constant.This is becoming crucial as people focus on serving larger and larger models. Image found on LinkedIn.Distillation is a powerful technique, but a couple things about it are quite mystical. The purpose of this post is to: Provide a very high level explainer (but mostly refer to source papers) of distillation. Show that you can create a simple, linear e... Read More

Sketching Algorithms for Matrix Preconditioning in Neural Network Optimization

18 Oct 2023

IntroductionIn this blog post, I’ll provide data stream background, applied context, motivation, and an overview for my recent work, Sketchy, co-authored with Xinyi Chen, Y. Jennifer Sun, Rohan Anil, and Elad Hazan, which will be featured in NeurIPS 2023 proceedings.I really enjoyed working on this project because it simultaneously scratches different methodological itches of mine, from data stream sketching to online convex optimization. However, the algorithm introduced here was borne out o... Read More

Crinkle Crankle Optimization

08 Oct 2023

A serpentine wall, or crinkle crankle wall, may seem like a surprising structure to use for fences, but may end up being more efficient in terms of building material than a straight fence which must withstand the same horizontal forces.In a post which is the raison d’etre for this one, John D. Cook derives a formula for computing the arc length of a sinusoidal curve. By assuming that such a sinusoidally-shaped wall could withstand lateral forces as much as a straight wall would, had the strai... Read More

Non-convex First Order Methods

20 Jun 2017

Non-convex First Order MethodsThis is a high-level overview of the methods for first order local improvement optimization methods for non-convex, Lipschitz, (sub)differentiable, and regularized functions with efficient derivatives, with a particular focus on neural networks (NNs).\[\argmin_\vx f(\vx) = \argmin_\vx \frac{1}{n}\sum_{i=1}^nf_i(\vx)+\Omega(\vx)\]Make sure to read the general overview post first. I’d also reiterate as Moritz Hardt has that one should be wary of only looking at con... Read More

Neural Network Optimization Methods

19 Jun 2017

Neural Network Optimization MethodsThe goal of this post and its related sub-posts is to explore at a high level how the theoretical guarantees of the various optimization methods interact with non-convex problems in practice, where we don’t really know Lipschitz constants, the validity of the assumptions that these methods make, or appropriate hyperparameters. Obviously, a detailed treatment would require delving into intricacies of cutting-edge research. That’s not the point of this post, w... Read More