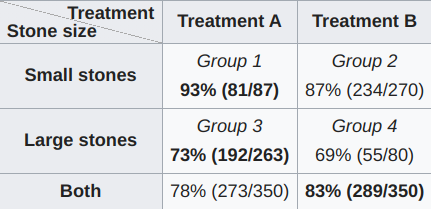$$ \newcommand{\bsth}{{\boldsymbol\theta}} \newcommand{\nptime}{\textsf{NP}} \newcommand{\ptime}{\textsf{P}} \newcommand{\disteq}{\overset{d}{=}} %linalg \newcommand{\mat}[1]{\begin{pmatrix} #1 \end{pmatrix}} \newcommand{\detmat}[1]{\begin{vmatrix} #1 \end{vmatrix}} \newcommand{\spanb}[1]{\text{span}\{ #1 \}} \DeclareMathOperator{\conv}{conv} % convex hull \DeclareMathOperator{\cone}{cone} \DeclareMathOperator{\vectorize}{vec} \DeclareMathOperator{\matricize}{mat} \DeclareMathOperator{\adj}{adj} \DeclareMathOperator{\diag}{diag} \DeclareMathOperator{\tr}{tr} \DeclareMathOperator{\rank}{rank} \DeclareMathOperator*{\argmin}{argmin} \DeclareMathOperator*{\proj}{proj} % brackets, norms, cardinalities \newcommand{\pa}[1]{ \left({#1}\right) } \newcommand{\ha}[1]{ \left[{#1}\right] } \newcommand{\ca}[1]{ \left\{{#1}\right\} } \newcommand{\inner}[1]{\left\langle #1 \right\rangle} \newcommand{\innercpy}[1]{\inner{ #1, #1 }} \newcommand{\norm}[1]{\left\| #1 \right\|} \newcommand{\abs}[1]{\left|{#1}\right|} \newcommand{\card}[1]{\left\vert{#1}\right\vert} % math vectors \newcommand{\va}{\textbf{a}} \newcommand{\vb}{\textbf{b}} \newcommand{\vc}{\textbf{c}} \newcommand{\vd}{\textbf{d}} \newcommand{\ve}{\textbf{e}} \newcommand{\vf}{\textbf{f}} \newcommand{\vg}{\textbf{g}} \newcommand{\vh}{\textbf{h}} \newcommand{\vi}{\textbf{i}} \newcommand{\vj}{\textbf{j}} \newcommand{\vk}{\textbf{k}} \newcommand{\vl}{\textbf{l}} \newcommand{\vm}{\textbf{m}} \newcommand{\vn}{\textbf{n}} \newcommand{\vo}{\textbf{o}} \newcommand{\vp}{\textbf{p}} \newcommand{\vq}{\textbf{q}} \newcommand{\vr}{\textbf{r}} \newcommand{\vs}{\textbf{s}} \newcommand{\vt}{\textbf{t}} \newcommand{\vu}{\textbf{u}} \newcommand{\vv}{\textbf{v}} \newcommand{\vw}{\textbf{w}} \newcommand{\vx}{\textbf{x}} \newcommand{\vy}{\textbf{y}} \newcommand{\vz}{\textbf{z}} \newcommand{\vzero}{\textbf{0}} \newcommand{\vone}{\textbf{1}} \newcommand{\valpha}{{\boldsymbol\alpha}} \newcommand{\vepsilon}{{\boldsymbol\epsilon}} \newcommand{\vnu}{{\boldsymbol\nu}} \newcommand{\vpi}{{\boldsymbol\pi}} \newcommand{\veta}{{\boldsymbol\eta}} \newcommand{\vsigma}{ {\boldsymbol\sigma}} \newcommand{\vbeta}{ {\boldsymbol\beta}} \newcommand{\vtheta}{ {\boldsymbol\theta}} \newcommand{\vdelta}{ {\boldsymbol\delta}} \newcommand{\vlambda}{ {\boldsymbol\lambda}} \newcommand{\vmu}{ {\boldsymbol\mu}} % common math sets \newcommand{\Z}{\mathbb{Z}} \newcommand{\R}{\mathbb{R}} \newcommand{\C}{\mathbb{C}} \newcommand{\N}{\mathbb{N}} \newcommand{\Q}{\mathbb{Q}} \newcommand{\F}{\mathbb{F}} \newcommand{\T}{\mathbb{T}} % limits \def\sumn{\sum_{n=0}^\infty} \def\limn{\lim_{n\rightarrow\infty}} \def\prodn{\prod_{n=0}^\infty} % mathcal \newcommand{\mcA}{\mathcal{A}} \newcommand{\mcB}{\mathcal{B}} \newcommand{\mcC}{\mathcal{C}} \newcommand{\mcD}{\mathcal{D}} \newcommand{\mcE}{\mathcal{E}} \newcommand{\mcF}{\mathcal{F}} \newcommand{\mcG}{\mathcal{G}} \newcommand{\mcH}{\mathcal{H}} \newcommand{\mcI}{\mathcal{I}} \newcommand{\mcJ}{\mathcal{J}} \newcommand{\mcK}{\mathcal{K}} \newcommand{\mcL}{\mathcal{L}} \newcommand{\mcM}{\mathcal{M}} \newcommand{\mcN}{\mathcal{N}} \newcommand{\mcO}{\mathcal{O}} \newcommand{\mcP}{\mathcal{P}} \newcommand{\mcQ}{\mathcal{Q}} \newcommand{\mcR}{\mathcal{R}} \newcommand{\mcS}{\mathcal{S}} \newcommand{\mcT}{\mathcal{T}} \newcommand{\mcU}{\mathcal{U}} \newcommand{\mcV}{\mathcal{V}} \newcommand{\mcW}{\mathcal{W}} \newcommand{\mcX}{\mathcal{X}} \newcommand{\mcY}{\mathcal{Y}} \newcommand{\mcZ}{\mathcal{Z}} % distribs, probability \newcommand{\disteq}{\overset{d}{=}} \newcommand\independent{\perp \!\!\! \perp} \DeclareMathOperator{\Laplace}{Laplace} \DeclareMathOperator{\Poisson}{Poisson} \DeclareMathOperator{\Exponential}{Exponential} \DeclareMathOperator{\Multinomial}{Multinomial} \DeclareMathOperator{\Bernoulli}{Bernoulli} \DeclareMathOperator{\Categorical}{Categorical} \DeclareMathOperator{\Uniform}{Uniform} \DeclareMathOperator{\Binomial}{Binomial} \DeclareMathOperator{\Hypergeometric}{Hypergeometric} \DeclareMathOperator{\GammaDist}{Gamma} \DeclareMathOperator{\NegativeBinomial}{NegativeBinomial} \DeclareMathOperator\sub{sub} \renewcommand{\d}[1]{\mathop{\mathrm{d} #1 }} \newcommand{\dkl}[2]{\mathop{D_\mathrm{KL}}\left({#1}\;\middle\|\;{#2}\right)} \newcommand{\sg}{\mathop{\mathrm{SG}}} \newcommand{\se}{\mathop{\mathrm{SE}}} %operators \DeclareMathOperator{\power}{{\mathcal{P}}} \DeclareMathOperator{\var}{var} \DeclareMathOperator{\cov}{cov} \DeclareMathOperator\mathProb{\mathbb{P}} \DeclareMathOperator\mathExp{\mathbb{E}} \DeclareMathOperator*\mathExpUnder{\mathbb{E}} \DeclareMathOperator*\fat{fat} \renewcommand{\P}{\mathProb} % need to overwrite stupid paragraph symbol \newcommand{\E}{\mathExp} % need to overwrite stupid paragraph symbol \newcommand{\set}[2]{ \left\{ #1 \,\middle|\, #2 \right\} } \newcommand{\CE}[2]{ \mathExp\left[ #1 \,\middle|\, #2 \right] } \renewcommand{\CP}[2]{ \mathProb\left\{ #1 \,\middle|\, #2 \right\} } $$

Articles by category: causal

---

graph-processing parallel distributed-systems online-learning machine-learning my-whitepapers hardware-acceleration interview-question tools optimization deep-learning numpy-gems joke-post philosophy causal statistics numpy tricks history llm pretraining

---

A Broader Emergence (Simpson's part 3 of 3)

01 Jun 2020

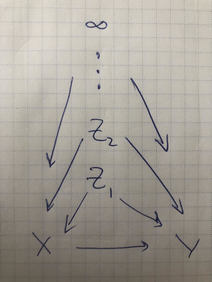
One neat takeaway from the previous post was really around the structure of what we were doing.What did it take for the infinite DAG we were building to become a valid probability distribution?We can throw some things out there that were necessary for its construction. The infinite graph needed to be a DAG We needed inductive “construction rules” $\alpha,\beta$ where we could derive conditional kernels from a finite subset of infinite parents to a larger subset of the infinite parents. The... Read More

An Infinite Simpson's Paradox (Simpson's part 2 of 3)

01 May 2020

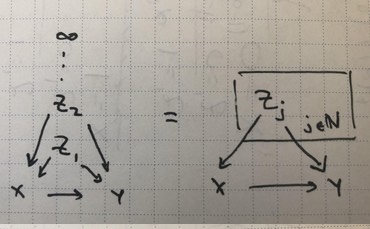
This is Problem 9.11 in Elements of Causal Inference._Construct a single Bayesian network on binary $X,Y$ and variables $\{Z_j\}_{j=1}^\infty$ where the difference in conditional expectation,\[\begin{align}\Delta_j(\vz_{\le j}) &=\\& \CE{Y}{X=1, Z_{\le j}=\vz_{\le j}}-\\& \CE{Y}{X=0, Z_{\le j}=\vz_{\le j}}\,\,,\end{align}\]satisfies $\DeclareMathOperator\sgn{sgn}\sgn \Delta_j=(-1)^{j}$ and $\abs{\Delta_j}\ge \epsilon_j$ for some fixed $\epsilon_j>0$. $\Delta_0$ is unconstrained... Read More

Observational Causal Inference (Simpson's part 1 of 3)

01 Apr 2020

In most data analysis, especially in business contexts, we’re looking for answers about how we can do better. This implies that we’re looking for a change in our actions that will improve some measure of performance.There’s an abundance of passively collected data from analytics. Why not point fancy algorithms at that?In this post, I’ll introduce a counterexample showing why we shouldn’t be able to extract such information easily.Simpson’s ParadoxThis has been explained many times, so I’ll be... Read More