Articles by category: tools

I’ve added heavy hitters functionality to the dsrs crate (in addition to a variant of Count-Min). It’s another streaming algorithm which helps us find the most popular repeated lines in a stream. In this blog post, we’ll see how this approximate algorithm saves memory over an exact approach.For instance, maybe we have access logs which contain IP addresses like so:1.1.1.13.1.2.31.1.1.14.2.1.21.1.1.1where there could be millions of unique IP addresses accessing our server, but we’d only be int... Read More

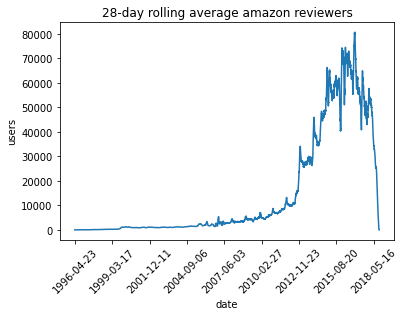
To show off a recent command line tool for sketching, dsrs, let’s plot the rolling 28-day average daily count of active reviewers on Amazon.The raw data here is item,user,rating,timestamp so this would map to a sophisticated GROUP BY with a COUNT DISTINCT over 28-day windows in SQL. But since the data’s only available as CSV, how can we get to the same answer? If we’re just interested in an approximate solution, can we do this without using a bunch of memory or custom (shuffle-inducing…) slid... Read More

Lots of sparse datasets are kept around in a convenient text format called SVMlight. It’s easy to manipulate with unix tools and very easily compressed so it’s perfect to distribute.However, the main way that’s available to access this format in python is dreadfully slow due to a natural lack of parallelism. svm2csr is a quick python package I wrote with a rust extension that parallelizes SVMlight parsing for faster loads in python. Check it out!P.S., here’s what this format looks like:-1 2:1... Read More

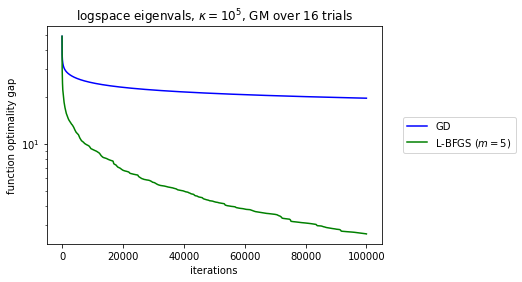
Curiously, the original L-BFGS convergence proof essentially reduces the L-BFGS iteration to GD. This establishes L-BFGS converges globally for sufficiently regular functions and also that it has local linear convergence, just like GD, for smooth and strongly convex functions.But if you look carefully at the proof, the construction is very strange: the more memory L-BFGS uses the less it looks like GD, the worse the smoothness constants are for the actual local rate of convergence. I go to in... Read More

This notebook comes from my Linear Regression Analysis notes.In the ordinary least squares setting, we model our outputs \(\mathbf{y}=X\boldsymbol\beta+\boldsymbol\varepsilon \) where \(\boldsymbol\varepsilon\sim N(\mathbf{0}, \sigma^2 I) \), with \(\boldsymbol\beta,\sigma^2 \) unknown.As a result the OLS fit \(\hat{\boldsymbol\beta}\sim N\left((X^\top X)^{-1}X^\top \mathbf{y},\sigma^2 (X^\top X)^{-1}\right) \) (an distribution with an unknown variance scaling factor which we must still S... Read More

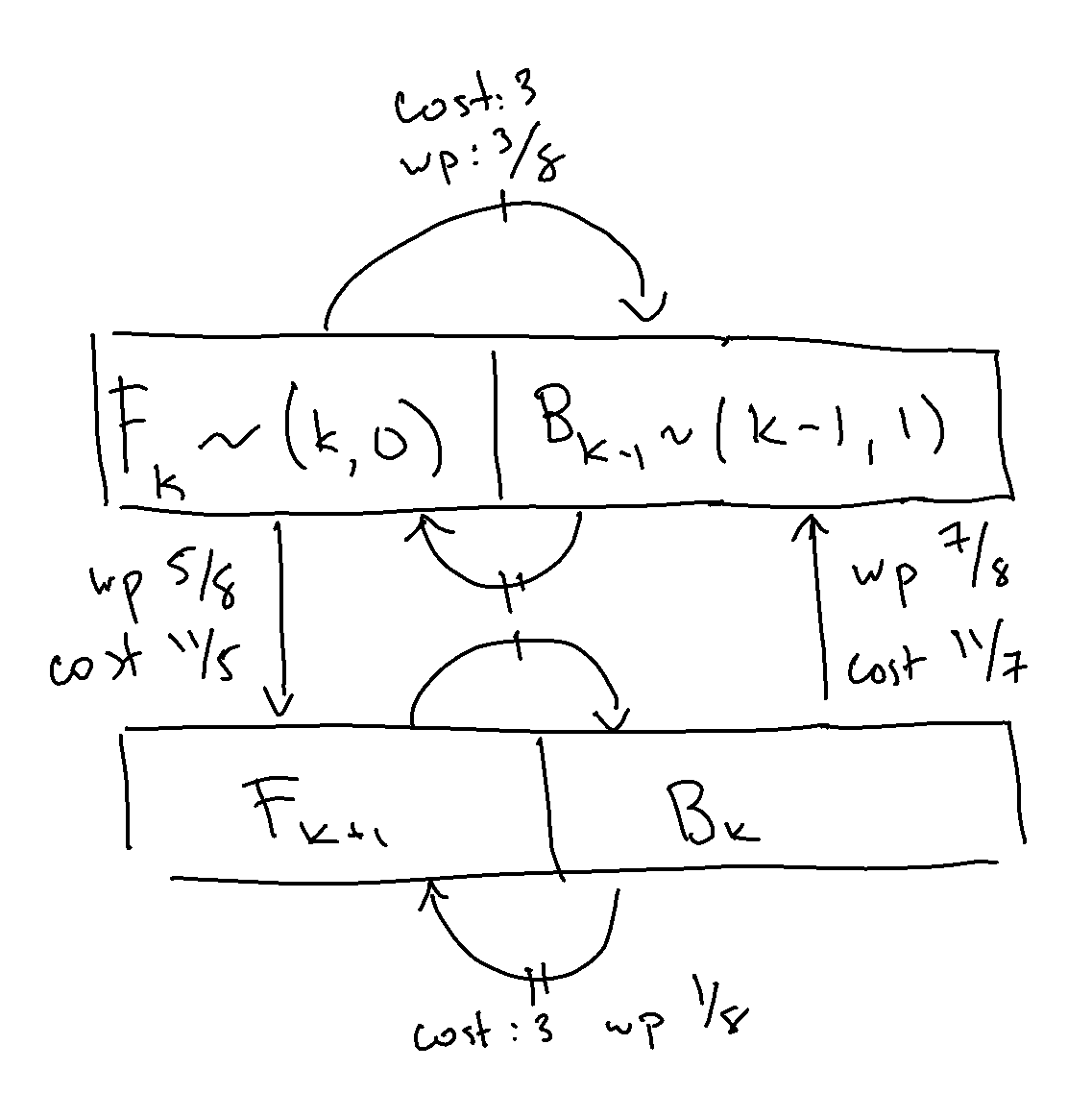
Last time, we discussed the RCT2 problem, which we won’t delve into in great detail, but at a high level, we have an inductively defined Markov chain, parameterized by \(n \), with special start and end states and the following outgoing arrows, such that for \(k\in[n] \), we have the following transition dynamics:from IPython.display import ImageImage(filename='transitions.png') We already went over how to solve the expected hitting time for the end state for a given, known \(n \). We now ... Read More

Roller Coaster Tycoon 2 (RCT2) ProblemIn Roller Coaster Tycoon 2, you play as the owner of an amusement park, building rides to attract guests. One ride you can build is a maze. It turns out that, for visual appeal, guests traverse mazes using a stochastic algorithm.Marcel Vos made an entertaining video describing the algorithm, which has in turn spawned an HN thread and Math SE post.I really enjoyed solving the problem and wanted to share the answer as well as some further thoughts.Mazes in ... Read More

In the previous post, we discussed a particular quantity, \(\mathbb{P}\{X=1\} \), where \(X \) follows a Poisson Binomial distribution, parameterized by \(\{p_j\}_{j=1}^n \). This means that \(X=\sum_jX_j \), where \(X_j \) are Bernoulli- \(p_j \) independent random variables.We came up with an \(O(1) \) memory and \(O(n) \) time approach to computing the desired probability, and gave an example where even the best approximations can be poor.What about a more general question? Let’s ta... Read More

This article investigates a fun thought experiment about the Poisson-Binomial distribution.Let’s imagine we’re designing a large hash table. We know up-front we’re going to get \(n \) distinct keys, so let’s number them \(j\in [n] \).Ahead of time, we’re allowed to see the set of hashes the \(j \)-th key will belong to. It is allowed to take on one of \(c_j \) distinct hashes, \(S_j=\{h_1, \cdots, h_{c_j}\}\subset\mathbb{N} \), where at run time the real hash is sampled uniformly (and in... Read More

Much of scientific computing revolves around the manipulation of indices. Most formulas involve sums of things and at the core of it the formulas differ by which things we’re summing.Being particularly clever about indexing helps with that. A complicated example is the FFT. A less complicated example is computing the inverse of a permutation:import numpy as npnp.random.seed(1234)x = np.random.choice(10, replace=False, size=10)s = np.argsort(x)inverse = np.empty_like(s)inverse[s] = np.arange(l... Read More

When reading, I prefer paper to electronic media. Unfortunately, a lot of my reading involves manuscripts from 8 to 100 pages in length, with the original document being an electronic PDF.Double-sided printing works really well to resolve this issue partway. It lets me convert PDFs into paper documents, which I can focus on. This works great up to 15 pages. I print the page out and staple it. I’ve tried not-stapling the printed pages before, but then the individual papers frequently get out o... Read More

PRNGsTrying out something new here with a Jupyter notebook blog post. We’ll keep this short. Let’s see how it goes!In this episode, we’ll be exploring random number generators.Usually, you use psuedo-random number generators (PRNGs) to simulate randomness for simulations. In general, randomness is a great way of avoiding doing integrals because it’s cheaper to average a few things than integrate over the whole space, and things tend to have accurate averages after just a few samples… This is ... Read More

Making LavenderI’ve tried using Personal Capital and Mint to monitor my spending, but I wasn’t happy with what those tools offered.In short, I was looking for a tool that: requires no effort on my part to get value out of (I don’t want to set budgets, I don’t even want the overhead of logging in to get updates) would tell me how much I’m spending would tell me why I’m spending this much would tell me if anything’s changedAll the tools out there are in some other weird market of “account m... Read More

Numpy Gems 1: Approximate Dictionary Encoding and Fast Python MappingWelcome to the first installment of Numpy Gems, a deep dive into a library that probably shaped python itself into the language it is today, numpy.I’ve spoken extensively on numpy (HN discussion), but I think the library is full of delightful little gems that enable perfect instances of API-context fit, the situation where interfaces and algorithmic problem contexts fall in line oh-so-nicely and the resulting code is clean, ... Read More

Beating TensorFlow Training in-VRAMIn this post, I’d like to introduce a technique that I’ve found helps accelerate mini-batch SGD training in my use case. I suppose this post could also be read as a public grievance directed towards the TensorFlow Dataset API optimizing for the large vision deep learning use-case, but maybe I’m just not hitting the right incantation to get tf.Dataset working (in which case, drop me a line). The solution is to TensorFlow harder anyway, so this shouldn’t reall... Read More

Jupyter TricksHere’s a list of my top-used Juypter tricks, and what they do.UII find the UI to be intuitive, Help > User Interface Tour describes more. There are command (enter by pressing the escape button or clicking outside of a cell) and edit (enter by typing in a cell) modes. You can tell you’re in edit mode if the “pencil” corner indicator is present:It’s also faster to use the commands as listed in Help > Keyboard Shortcuts; with those you can also remove the toolbar with View &g... Read More