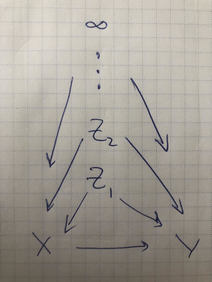
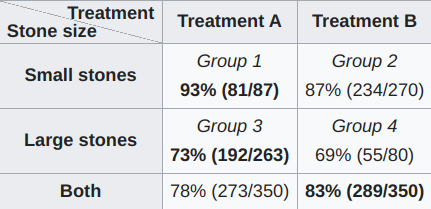This is Problem 9.11 in Elements of Causal Inference. _Construct a single Bayesian network on binary $X,Y$ and variables $\{Z_j\}_{j=1}^\infty$ where the difference in conditional expectation, \[\begin{align} \Delta_j(\vz_{\le j}) &=\\ & \CE{Y}{X=1, Z_{\le j}=\vz_{\le j}}-\\ & \CE{Y}{X=0, Z_{\le j}=\vz_{\le j}}\,\,, \end{align}\] satisfies $\DeclareMathOperator\sgn{sgn}\sgn \Delta_j=(-1)^{j}$ and $\abs{\Delta_j}\ge \epsilon_j$ for some fixed $\epsilon_j>0$. $\Delta_0$ is unc...
In most data analysis, especially in business contexts, we’re looking for answers about how we can do better. This implies that we’re looking for a change in our actions that will improve some measure of performance. There’s an abundance of passively collected data from analytics. Why not point fancy algorithms at that? In this post, I’ll introduce a counterexample showing why we shouldn’t be able to extract such information easily. Simpson’s Paradox This has been explained many times, so...
Much of scientific computing revolves around the manipulation of indices. Most formulas involve sums of things and at the core of it the formulas differ by which things we’re summing. Being particularly clever about indexing helps with that. A complicated example is the FFT. A less complicated example is computing the inverse of a permutation: import numpy as np np.random.seed(1234) x = np.random.choice(10, replace=False, size=10) s = np.argsort(x) inverse = np.empty_like(s) inverse[s] = np...
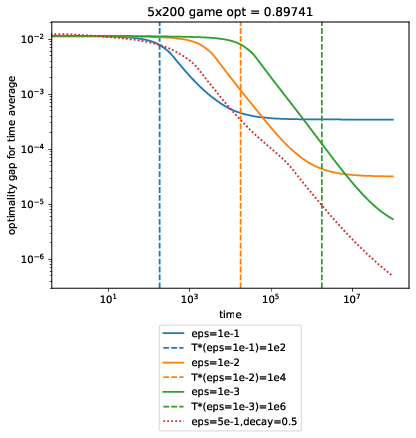
Multiplicative weights is a simple, randomized algorithm for picking an option among \(n\) choices against an adversarial environment. The algorithm has widespread applications, but its analysis frequently introduces a learning rate parameter, \(\epsilon\), which we’ll be trying to get rid of. In this first post, we introduce multiplicative weights and make some practical observations. We follow Arora’s survey for the most part. Problem Setting We play \(T\) rounds. On the \(t\)-th round,...
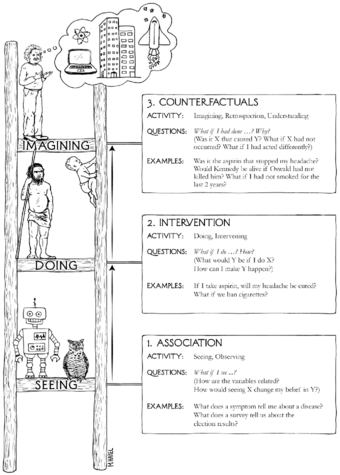
If you read Judea Pearl’s The Book of Why, it makes it seem like exercising observational statistics makes you an ignoramus. Look at the stupid robot: Pearl and Jonas Peters (in Elements of Causal Inference) both make a strong distinction, it seems at the physical level, between causal and statistical learning. Correlation is not causation, as it goes. From a deeply (Berkeley-like) skeptical lens, where all that we can be sure of is what we observe, it seems that we nonetheless can recove...
When reading, I prefer paper to electronic media. Unfortunately, a lot of my reading involves manuscripts from 8 to 100 pages in length, with the original document being an electronic PDF. Double-sided printing works really well to resolve this issue partway. It lets me convert PDFs into paper documents, which I can focus on. This works great up to 15 pages. I print the page out and staple it. I’ve tried not-stapling the printed pages before, but then the individual papers frequently get out...
PRNGs Trying out something new here with a Jupyter notebook blog post. We’ll keep this short. Let’s see how it goes! In this episode, we’ll be exploring random number generators. Usually, you use psuedo-random number generators (PRNGs) to simulate randomness for simulations. In general, randomness is a great way of avoiding doing integrals because it’s cheaper to average a few things than integrate over the whole space, and things tend to have accurate averages after just a few samples… Th...
Compressed Sensing and Subgaussians Candes and Tao came up with a broad characterization of compressed sensing solutions a while ago. Partially inspired by a past homework problem, I’d like to explore an area of this setting. This post will dive into the compressed sensing context and then focus on a proof that squared subgaussian random variables are subexponential (the relation between the two will be explained). Compressed Sensing For context, we’re interested in the setting where we o...
Making Lavender I’ve tried using Personal Capital and Mint to monitor my spending, but I wasn’t happy with what those tools offered. In short, I was looking for a tool that: requires no effort on my part to get value out of (I don’t want to set budgets, I don’t even want the overhead of logging in to get updates) would tell me how much I’m spending would tell me why I’m spending this much would tell me if anything’s changed All the tools out there are in some other weird market ...
FAISS, Part 1 FAISS is a powerful GPU-accelerated library for similarity search. It’s available under MIT on GitHub. Even though the paper came out in 2017, and, under some interpretations, the library lost its SOTA title, when it comes to a practical concerns: the library is actively maintained and cleanly written. it’s still extremely competitive by any metric, enough so that the bottleneck for your application won’t likely be in FAISS anyway. if you bug me enough, I may fix my one...
FAISS, Part 2 I’ve previously motivated why nearest-neighbor search is important. Now we’ll look at how FAISS solves this problem. Recall that you have a set of database vectors \(\{\textbf{y}_i\}_{i=0}^\ell\), each in \(\mathbb{R}^d\). You can do some prep work to create an index. Then at runtime I ask for the \(k\) closest vectors in \(L^2\) distance. Formally, we want the set \(L=\text{$k$-argmin}_i\norm{\textbf{x}-\textbf{y}_i}\) given \(\textbf{x}\). The main paper contributions in t...
BERT In the last two posts, we reviewed Deep Learning and The Transformer. Now we can discuss an interesting advance in NLP, BERT, Bidirectional Encoder Representations from Transformers (arxiv link). BERT is a self-supervised method, which uses just a large set of unlabeled textual data to learn representations broadly applicable for different language tasks. At a high level, BERT’s pre-training objective, which is what’s used to get its parameters, is a Language modelling (LM) problem. L...
BERT Prerequisite 2: The Transformer In the last post, we took a look at deep learning from a very high level (Part 1). Here, we’ll cover the second and final prerequisite for setting the stage for discussion about BERT, the Transformer. The Transformer is a novel sequence-to-sequence architecture proposed in Google’s Attention is All You Need paper. BERT builds on this significantly, so we’ll discuss here why this architecture was important. The Challenge Recall the language of the previ...
A Modeling Introduction to Deep Learning In this post, I’d like to introduce you to some basic concepts of deep learning (DL) from a modeling perspective. I’ve tended to stay away from “intro” style blog posts because: There are so, so many of them. They’re hard to keep in focus. That said, I was presenting on BERT for a discussion group at work. This was our first DL paper, so I needed to warm-start a technical audience with a no-frills intro to modeling with deep nets. So here we a...
Numpy Gems 1: Approximate Dictionary Encoding and Fast Python Mapping Welcome to the first installment of Numpy Gems, a deep dive into a library that probably shaped python itself into the language it is today, numpy. I’ve spoken extensively on numpy (HN discussion), but I think the library is full of delightful little gems that enable perfect instances of API-context fit, the situation where interfaces and algorithmic problem contexts fall in line oh-so-nicely and the resulting code is cle...
Subgaussian Concentration This is a quick write-up of a brief conversation I had with Nilesh Tripuraneni and Aditya Guntuboyina a while ago that I thought others might find interesting. This post focuses on the interplay between two types of concentration inequalities. Concentration inequalities usually describe some random quantity \(X\) as a constant \(c\) which it’s frequently near (henceforth, \(c\) will be our stand-in for some constant which possibly changes equation-to-equation). Bas...
Beating TensorFlow Training in-VRAM In this post, I’d like to introduce a technique that I’ve found helps accelerate mini-batch SGD training in my use case. I suppose this post could also be read as a public grievance directed towards the TensorFlow Dataset API optimizing for the large vision deep learning use-case, but maybe I’m just not hitting the right incantation to get tf.Dataset working (in which case, drop me a line). The solution is to TensorFlow harder anyway, so this shouldn’t rea...
Deep Learning Learning Plan This is my plan to on-board myself with recent deep learning practice (as of the publishing date of this post). Comments and recommendations via GitHub issues are welcome and appreciated! This plan presumes some probability, linear algebra, and machine learning theory already, but if you’re following along Part 1 of the Deep Learning book gives an overview of prerequisite topics to cover. My notes on these sources are publicly available, as are my experiments. ...
Non-convex First Order Methods This is a high-level overview of the methods for first order local improvement optimization methods for non-convex, Lipschitz, (sub)differentiable, and regularized functions with efficient derivatives, with a particular focus on neural networks (NNs). \[ \argmin_\vx f(\vx) = \argmin_\vx \frac{1}{n}\sum_{i=1}^nf_i(\vx)+\Omega(\vx) \] Make sure to read the general overview post first. I’d also reiterate as Moritz Hardt has that one should be wary of only lookin...